خواجه نصیرالدین طوسی ریاضیدان و منجم ایرانی برای توضیح دادن حرکت ظاهری سیارات ،دو کره را در نظر گرفته بود که یکی در داخل دیگری دوران می کند. اگر دایره‌ای کوچک داخل دایره‌ای بزرگ‌تر که شعاعی دو برابر آن دارد محاط و بر آن مماس شود، با دوران دایره کوچک روی محیط دایره بزرگ هر نقطه‌ای از دایرهٔ کوچک در مسیر حرکت خود قطری منحصربه‌فرد از دایره بزرگ را رسم می‌کند. ا.س.کندی مورخ امریکایی ریاضیات اسلامی این ساز و کار را جفت طوسی نامیده است.
در توضیح جفت طوسی از خواجه نصیر
خواجه نصیرالدین طوسی نخستین کسی بود که در کتاب کشف القناع عن اسرار شکل القطاع، مثلثات را بدون توسل به قضیه منلائوس یا نجوم توسعه بخشید و آن را در پیش‌گفتار علم نجوم معرفی کرد.
آثار ابن سینا:
کتاب زاویه
مقاطع مخروطی
Conic section
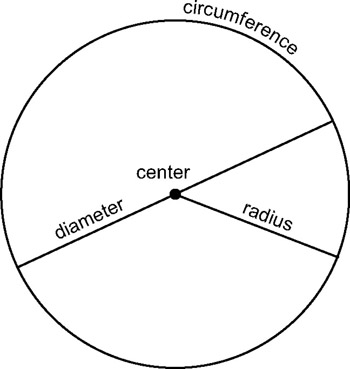
مقطع مخروطی یک منحنی است که از تقاطع یک صفحه و مخروط می تواند به وجود بیاید.
در ریاضیات سهمی (شلجمی) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. سهمی یکی از مقاطع مخروطی است.
A parabola is a two-dimensional, mirror-symmetrical curve, which is approximately U-shaped.
مقاطع مخروطی را می‌توان به کمک دو کانون، یک کانون و یک خط هادی، و یا یک کانون و یک دایره تعریف کرد.
نخستین ابداع کننده نظریهٔ پرگار تام بوده است. این پرگار برای رسم تمام مقاطع مخروطی طراحی شده بوده است.
این ابزار از دو بازوی متحرک تشکیل شده است. بازوی نخست، محور یا خط مرکز نامیده می‌شود و بر صفحه‌ای به نام قاعدهٔ پرگار عمود است، این محور در یکی از صفحات عمود بر قاعده، می‌تواند حرکت کند و زاویه‌ای موسوم به زاویهٔ مرکز، α، را تشکیل دهد. بازوی دوم بر بالای محور قرار دارد و خط رأس نام دارد و سه گونه حرکت می‌تواند داشته باشد. زاویهٔ خط رأس با زاویهٔ محور، β، زاویهٔ رأس نام دارد. حرکت نخست خط رأس در همان صفحه‌ای که محور نیز می‌تواند حرکت کند، انجام شدنی است؛ حرکت دوم حول محور صورت می‌گیرد. حرکت سوم یک حرکت کشویی است، یعنی طول بازوی دوم متغیّر است در واقع نوک آن که وظیفهٔ ترسیم را به عهده دارد، می‌تواند از یک قسمت لوله‌ای شکل بیرون بلغزد. سرشت خـَم ترسیمی به دو زاویهٔ یاد شده بستگی دارد.
پرگار تام کوهی، از نسخه‌ای در استانبول
ریاضیدان یونان باستان
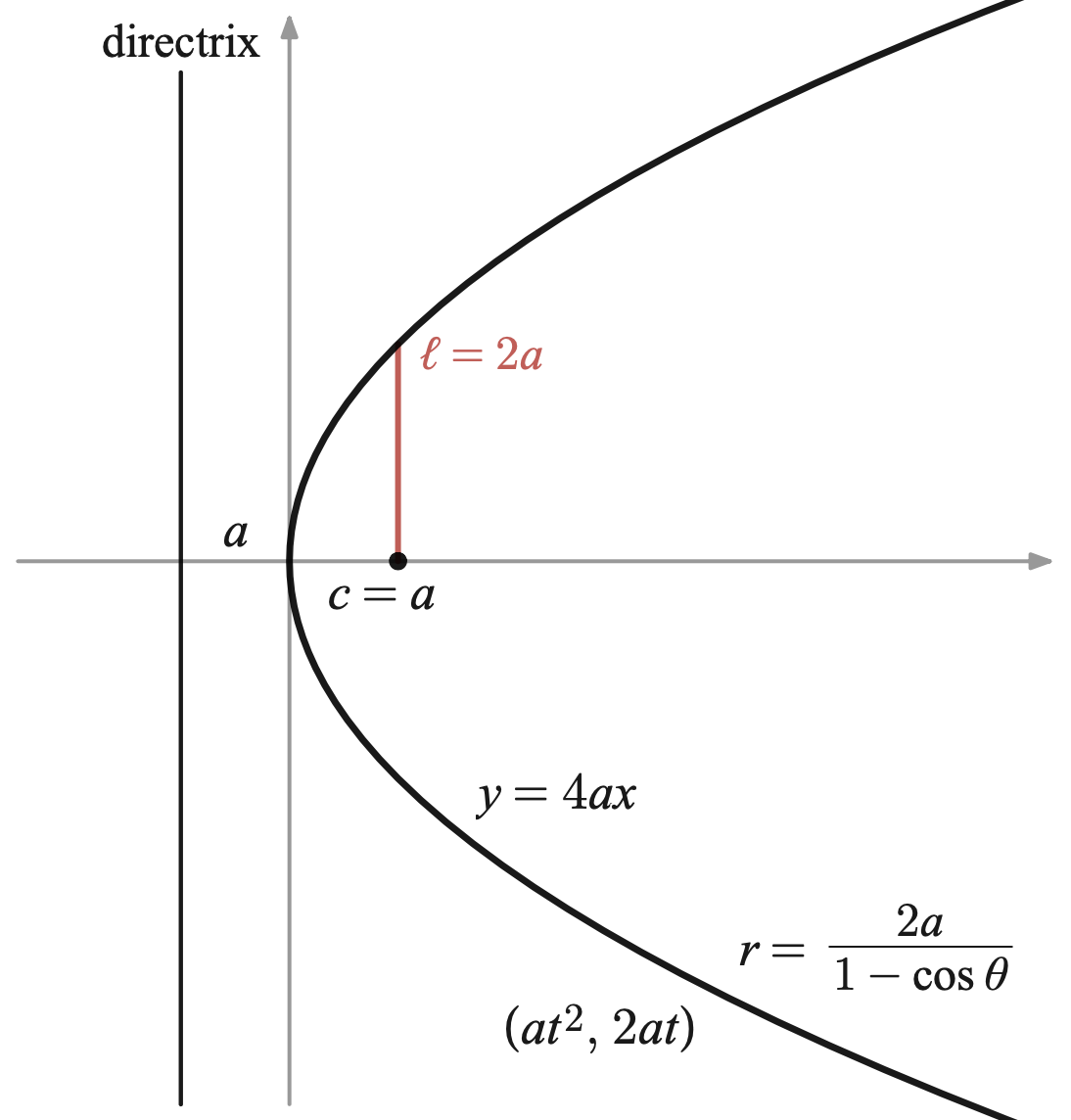
سهمی را جهت حل مسئله تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض
است فقط با استفاده از خط‌کش و پرگار)، مورد مطالعه قرار داد.
خواجه نصیرالدین طوسی ریاضیدان و منجم ایرانی برای توضیح دادن حرکت ظاهری سیارات ،دو کره را در نظر گرفته بود که یکی در داخل دیگری دوران می کند. اگر دایره‌ای کوچک داخل دایره‌ای بزرگ‌تر که شعاعی دو برابر آن دارد محاط و بر آن مماس شود، با دوران دایره کوچک روی محیط دایره بزرگ هر نقطه‌ای از دایرهٔ کوچک در مسیر حرکت خود قطری منحصربه‌فرد از دایره بزرگ را رسم می‌کند. ا.س.کندی مورخ امریکایی ریاضیات اسلامی این ساز و کار را جفت طوسی نامیده است.
|
| در توضیح جفت طوسی از خواجه نصیر |
خواجه نصیرالدین طوسی نخستین کسی بود که در کتاب کشف القناع عن اسرار شکل القطاع، مثلثات را بدون توسل به قضیه منلائوس یا نجوم توسعه بخشید و آن را در پیش‌گفتار علم نجوم معرفی کرد.
آثار ابن سینا:
کتاب زاویه
کتاب اقلیدس
کتاب الارتماطیقی
کتاب علم هیئت
کتاب المجسطی
کتاب جامع البدایع
کتاب طبیعی
مقاطع مخروطی
Conic section
مقطع مخروطی یک منحنی است که از تقاطع یک صفحه و مخروط می تواند به وجود بیاید.
در ریاضیات سهمی (شلجمی) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. سهمی یکی از مقاطع مخروطی است.
مقاطع مخروطی را می‌توان به کمک دو کانون، یک کانون و یک خط هادی، و یا یک کانون و یک دایره تعریف کرد.
در ریاضیات سهمی (شلجمی) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. سهمی یکی از مقاطع مخروطی است.
A parabola is a two-dimensional, mirror-symmetrical curve, which is approximately U-shaped.
نخستین ابداع کننده نظریهٔ پرگار تام بوده است. این پرگار برای رسم تمام مقاطع مخروطی طراحی شده بوده است.
این ابزار از دو بازوی متحرک تشکیل شده است. بازوی نخست، محور یا خط مرکز نامیده می‌شود و بر صفحه‌ای به نام قاعدهٔ پرگار عمود است، این محور در یکی از صفحات عمود بر قاعده، می‌تواند حرکت کند و زاویه‌ای موسوم به زاویهٔ مرکز، α، را تشکیل دهد. بازوی دوم بر بالای محور قرار دارد و خط رأس نام دارد و سه گونه حرکت می‌تواند داشته باشد. زاویهٔ خط رأس با زاویهٔ محور، β، زاویهٔ رأس نام دارد. حرکت نخست خط رأس در همان صفحه‌ای که محور نیز می‌تواند حرکت کند، انجام شدنی است؛ حرکت دوم حول محور صورت می‌گیرد. حرکت سوم یک حرکت کشویی است، یعنی طول بازوی دوم متغیّر است در واقع نوک آن که وظیفهٔ ترسیم را به عهده دارد، می‌تواند از یک قسمت لوله‌ای شکل بیرون بلغزد. سرشت خـَم ترسیمی به دو زاویهٔ یاد شده بستگی دارد.
|
| پرگار تام کوهی، از نسخه‌ای در استانبول |
ریاضیدان یونان باستان
سهمی را جهت حل مسئله تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض
است فقط با استفاده از خط‌کش و پرگار)، مورد مطالعه قرار داد.
در کتاب «اصول ریاضی
فلسفه طبیعی» نشان داد که اگر نیروی کشش میان اجسام آسمانی متناسب با معکوس
مجذور فاصله بین آن دو باشد، اجرامی که به دور یک جرم بزرگ می‌گرداند، یا باید حرکت
دایره‌ای، بیضوی، سهموی و یا هذلولوی داشته باشند. نیوتن از سهمی برای محاسبه مدار
شهاب سنگ‌ها استفاده کرد. امروزه می‌دانیم که اگر چه سهمی
مدل خوبی برای حرکت شهاب سنگ‌ها می‌باشد ولی این مدل از دقت بالایی برخوردار نیست و
بندرت مدار شهاب سنگ‌ها با دقت بسیار بالایی سهموی می‌باشند.
نشان داد که وقتی جسمی
را در هوا پرتاب می‌کنیم، مسیر حرکت آن سهموی می‌باشد.
این موضوع زمانی صحت
دارد که از مقاومت هوا و آثار چرخشی چشم پوشی شود.
نشان دادند که هنگامی
که نور به صورت موازی به یک آینه سهموی تابانده شود، پس از انعکاس در کانون آن جمع
می‌شود.
رسم چند ضلعی منتظم با پرگار
نشان دادند که هنگامی
که نور به صورت موازی به یک آینه سهموی تابانده شود، پس از انعکاس در کانون آن جمع
می‌شود.
سهمی را تصویر یک دایره
در نظر گرفت.
رسم چند ضلعی منتظم با پرگار
